Прямая и обратная геодезическая задача

Задача

Составить программу для решения прямой и обратной геодезических задач.

Прямая геодезическая задача состоит в том, что по координатам одного конца А (XА и YА) линии АВ, по дирекционному углу этой линии αАВ и ее горизонтальному проложению SАВ вычисляют координаты другого конца В этой линии (XВ YВ).

XB=XA+SABcos αАВ,

YB=YA+SABsin αАВ.

Обратная геодезическая задача состоит в том, что по координатам концов линии АВ вычисляют дирекционный угол и горизонтальное проложение этой линии. То есть известны: XA, YA, XB, YB. Надо вычислить αАВ и SАВ.

Компоненты

Имя

компонента

Свойства

компонент

Значение

Назначение

Form1

Caption

Прямая и обратная геодезические задачи

Заголовок формы

Label1

Caption

 

 

 

 

 

 

Visible

Обратная геодезическая задача — вычисление по координатам двух точек горизонтального проложения линии между ними и дирекционного угла

 

False

Справочная информация для пользователя программы

 

 

 

невидимый

Label2

Caption

 

Visible

XA

 

False

Подсказка пользователю

невидимый

Label3

Caption

 

Visible

YA

 

False

Подсказка пользователю

невидимый

Label4

Caption

 

Visible

XB

 

False

Подсказка пользователю

невидимый

Label5

Caption

 

Visible

YB

 

False

Подсказка пользователю

невидимый

Label6

Caption

 

 

Visible

Горизонтальное проложение линии АВ в метрах

 

False

Подсказка пользователю

 

невидимый

Label7

Caption

 

 

 

Visible

 

 

 

 

False

Поле для вывода горизонтального проложения

 

невидимый

Label8

Caption

 

 

Visible

Дирекционный угол (гр. мин. сек.)

 

False

Подсказка пользователю

 

невидимый

Label9

Caption

 

 

 

Visible

 

 

 

 

False

Поле для вывода дирекционного угла (градусы)

 

невидимый

Label10

Caption

 

 

 

Visible

 

 

 

 

False

Поле для вывода дирекционного угла (минуты)

 

невидимый

Label11

Caption

 

 

 

Visible

 

 

 

 

False

Поле для вывода дирекционного угла (секунды)

 

невидимый

Edit1

Text

 

Visible

…..

 

False

Поле для ввода координаты XА

невидимый

Edit2

Text

 

Visible

…..

 

False

Поле для ввода координаты YА

невидимый

Edit3

Text

 

Visible

…..

 

False

Поле для ввода координаты XB

невидимый

Edit4

Text

 

Visible

…..

 

False

Поле для ввода координаты YB

невидимый

Button1

Caption

ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА

Кнопка запускает на выполнение прямую геодезическую задачу

Button2

Caption

ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА

Кнопка делает видимыми поля для решения обратной геодезической задачи

Button3

Caption

ВЫХОД

Кнопка закрытия формы и выхода из программы

Button4

Caption

 

 

 

Visible

Вычислить

 

 

 

False

Кнопка вычисления обратной геодезической задачи

невидимый

Переменные

Обозначение в программе

Содержание

Тип

XA

Координата X точки А

вещественный

YA

Координата Y точки А

вещественный

XB

Координата X точки B

вещественный

YB

Координата Y точки B

вещественный

G

Часть дирекционного угла линии АВ в градусах

целый

M

Часть дирекционного угла линии АВ в минутах

целый

S

Часть дирекционного угла линии АВ в секундах

вещественный

L

Горизонтальное проложение лини АВ

вещественный

DX

Приращение координат по оси X

вещественный

DY

Приращение координат по оси Y

вещественный

DU

Дирекционный угол в градусах

вещественный

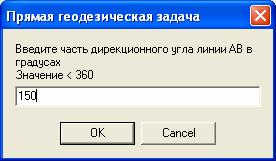
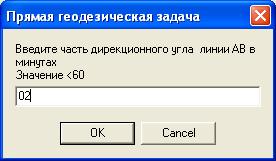
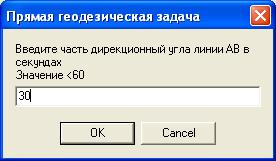
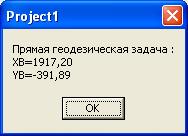
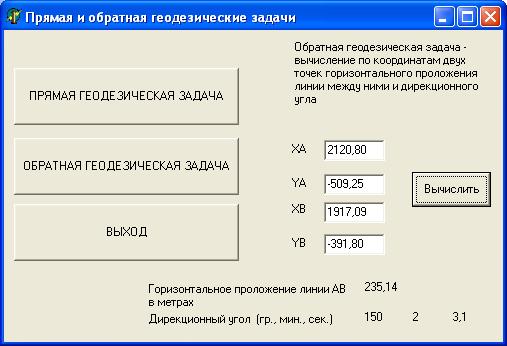
Замечание

При проектировании компонентов для решения обратной геодезической задачи на той же форме, свойство Visible компонентов целесообразно установить в положение False.

Текст модуля

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics,

Controls, Forms,

Dialogs, StdCtrls, Math;

{ библиотечный модуль Math нужно добавить в стандартный набор модулей для подключения математической библиотеки  }

………………………..

var

Form1: TForm1;

   XA,YA:Extended; //координаты точки A     Отпуск в Греции  www.landlady2009.narod.ru

XB,YB:Extended; // координаты точки B

G:Integer;    // дирекционный угол в градусах

M: Integer;   // часть дирекционного угла в минутах

S:Real;      // часть дирекционного угла в секундах

L:Extended;  // горизонтальное проложение линии AB

DX, DY:Extended;// приращения координат по осям X,Y

DU:Extended;// дирекционный угол в радианах

implementation

{$R *.dfm}

procedure TForm1.Button1Click(Sender: TObject);

begin

ShowMessage('Прямая геодезическая задача - определение координаты'+

' точки по координатам исходной точки, горизонтальному проложению '

+ ' и дирекционному углу.'+#13

+'Дирекционный угол задается в градусах, минутах и секундах. Коор-ты в метрах.');

// ввод координат исходной точки, дирекционного угла

// и горизонтального проложения линии AB из окон ввода

XA:=StrToFloat(InputBox('Прямая геодезическая задача',

'Введите координату X точки A','0'));

YA:=StrToFloat(InputBox('Прямая геодезическая задача',

'Введите координату Y точки A','0'));

G:=StrToInt(InputBox('Прямая геодезическая задача',

'Введите часть дирекционного угла линии AВ в градусах' +#13

+'Значение < 360','0'));

M:=StrToInt(InputBox('Прямая геодезическая задача',

'Введите часть дирекционного угла  линии AВ в минутах'+

#13+'Значение <60','0'));

S:=StrToFloat(InputBox('Прямая геодезическая задача',

'Введите часть дирекционный угла линии AВ в секундах' +#13+'Значение <60','0'));

L:=StrToFloat(InputBox('Прямая геодезическая задача',

'Введите горизонтальное проложение линии AВ в метрах','0'));

// вычисление координат точки B

// в ниже приведенном преобразовании можно использовать

//функцию преобразования DegTORad

XB:=XA+L*cos((g+m/60+s/3600)/180*pi);

YB:=YA+L*sin((g+m/60+s/3600)/180*pi);

{XB:=XA+L*cos(DegToRad(g+m/60+s/3600));

YB:=YA+L*sin(DegToRad (g+m/60+s/3600));}

//округление вычисленных координат

// до двух знаков после запятой

XB:=Trunc(XB*100+0.5)/100;

YB:=Trunc(YB*100+0.5)/100;

// вывод координат точки B окно сообщения

ShowMessage('Прямая геодезическая задача ' +#13 +'XB=' +FloatToStrF(XB,Fffixed,10,2)+ #13

 + 'YB='+FloatToStrF(YB,Fffixed,10,2))

end;

procedure TForm1.Button3Click(Sender: TObject);

begin

Form1.Close

end;

procedure TForm1.Button2Click(Sender: TObject);

begin

// сделать видимыми компоненты, относящиеся к обратной

 //геодезической задаче

Label1.Visible:=True;

Label2.Visible:=True;

Label3.Visible:=True;

Label4.Visible:=True;

Label5.Visible:=True;

Label6.Visible:=True;

Label7.Visible:=True;

Label8.Visible:=True;

Label9.Visible:=True;

Label10.Visible:=True;

Label11.Visible:=True;

Edit1.Visible:=True;

Edit2.Visible:=True;

Edit3.Visible:=True;

Edit4.Visible:=True;

// перенести фокус в первое поле ввода на форме

Edit1.SetFocus;

Button4.Visible:=True;

end;

procedure TForm1.Button4Click(Sender: TObject);

Var 

begin

// ввод координат точек A и B из полей ввода на форме

XA:=StrToFloat(Edit1.Text);

YA:=StrToFloat(Edit2.Text);

XB:=StrToFloat(Edit3.Text);

YB:=StrToFloat(Edit4.Text);

DX:=XB-XA;

DY:=YB-YA;

// вычисление горизонтального проложения линии AB

L:=Sqrt(Sqr(DX)+Sqr(DY));

// округление горизонтального проложения

// до двух знаков после запятой

L:=Trunc(L*100+0.5)/100;

// вычисление дирекционного угла и перевод

// его значения из радиан в градусы

DU:=ArcTan2(DY,DX)/Pi*180;

{в данном преобразовании можно было использовать функцию

RadToDeg: DU:= RadToDeg (ArcTan2(DY,DX));}

//ArcTan2(Y/X) - библиотечная функция находит угол X/Y

//в несущем квандарте по знакам X и Y от -Pi до Pi  в радианах.

//если угол со знаком минус к нему прибавляется 360 градусов

if DU<0 Then DU:=360+DU;

//выделение градусной части дирекционного угла

G:=Trunc(DU);

// выделение минутной части дирекционного угла

M:=Trunc((DU-G)*60);

// выделение секундной части дирекционного угла

S:=((DU-G)*60-M)*60;

{вывод горизонтального проложения и дирекционного угла в поля вывода}

Label7.Caption:=FloatToStrF(L,Fffixed,10,2);

Label9.Caption:=IntToStr(G);

Label10.Caption:=IntToStr(M);

Label11.Caption:=FloatToStrF(S,Fffixed,5,1);

end;

end.

Такие окна будут появляться на экране при выполнении проекта:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

To contact us:

 

E-mail:           landlad2002@mail.ru

Главная

В начало
Сайт создан в системе uCoz